How Does AI Learn? A Beginner’s Guide with Examples

This article explains how AI systems learn parameters from data, and how advances in compute, data and algorithms have enabled modern AI systems.

Learning parameters from data

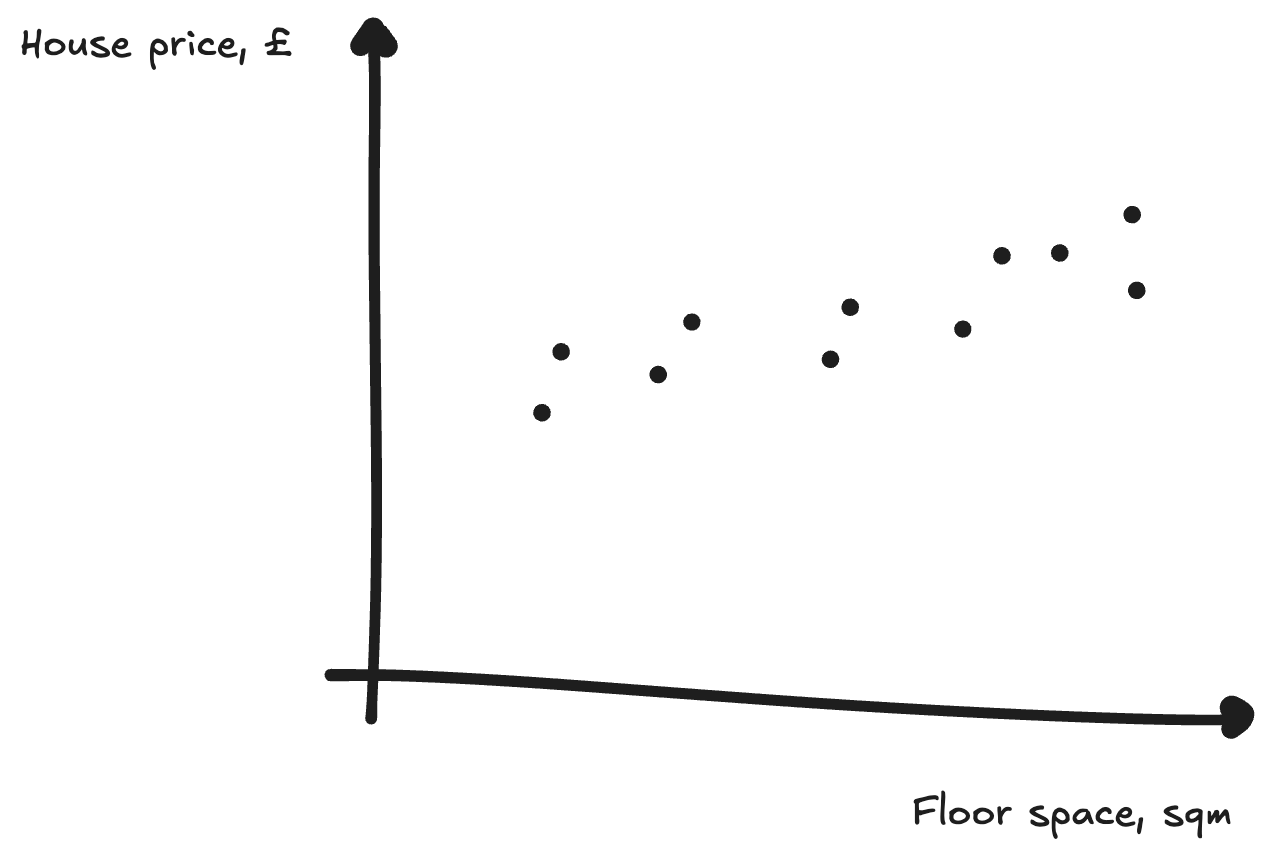
Imagine you’re an estate agent, and want to know how to price houses you’re selling. You have some basic data about previous sale prices, which looks like this:

What you might do to evaluate this is draw a line of best fit through the graph. This has the equation y = ax + b, where a and b are parameters.

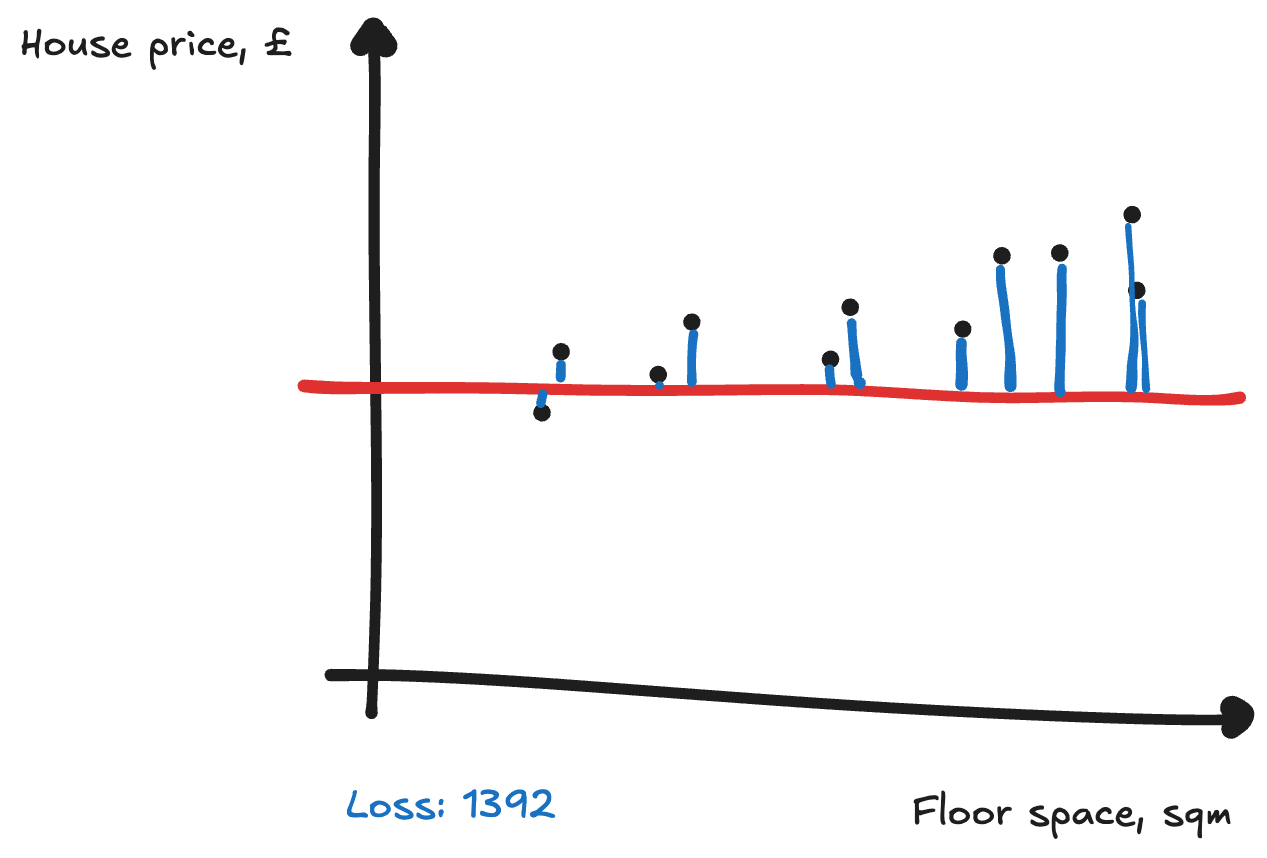
To find the parameters, you can use trial and improvement.[[1]] Perhaps you start by picking some numbers at random for our parameters, and see how well it does. To calculate how good it is, you can add up how far away the points are from the line. This measure of how far away we are is the loss, and you’ll want to decrease this (so the line is closer to the points).

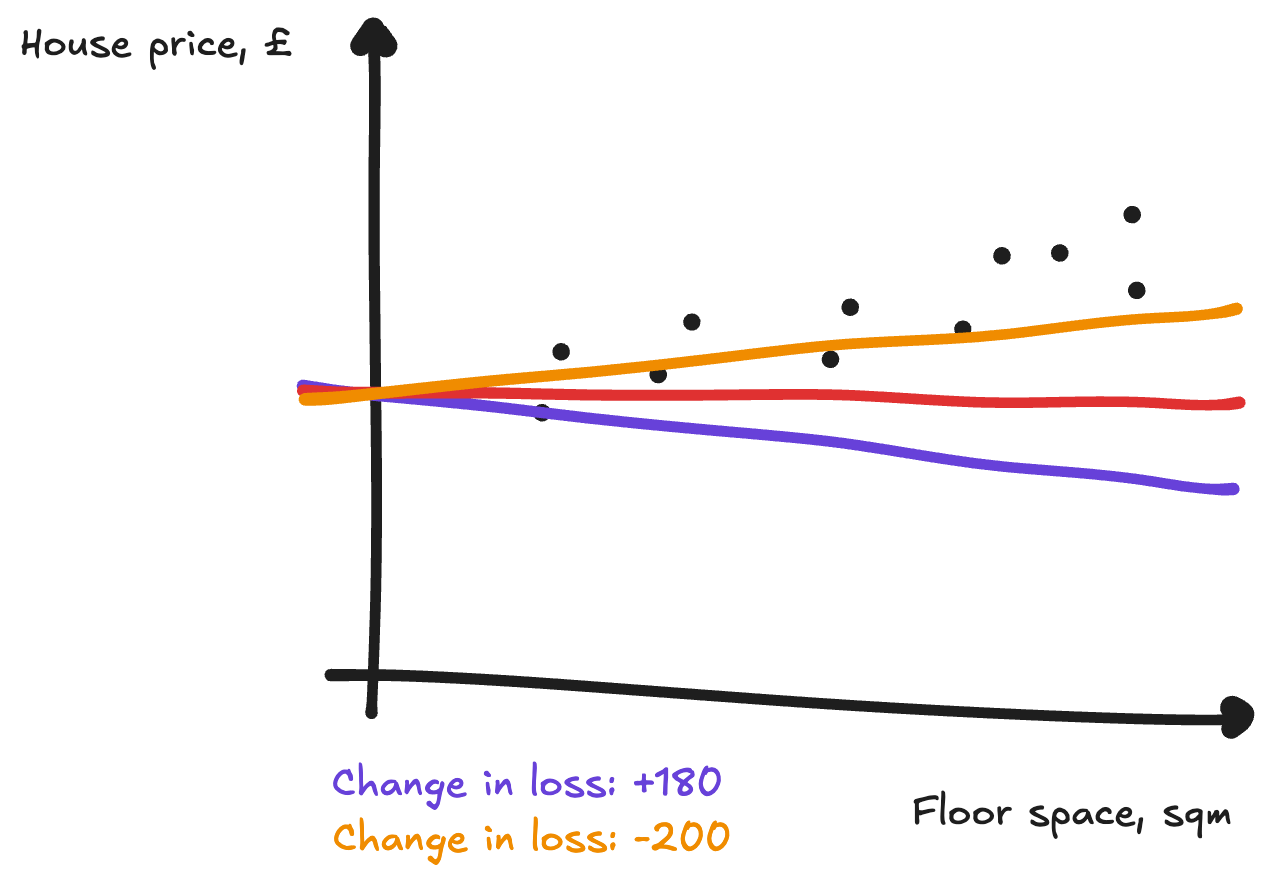
A classic method of trial and improvement is to tweak your guesses a little bit, and see if that makes things better. Here you try tweaking the a parameter up and down, and see whether it decreases the loss:

When a increased a little the loss went down. And when `a` decreased a little the loss went up. You should therefore increase a a little to make the loss go down. The relationship between changing a parameter and how much our loss changes is known as the gradient.[[2]]

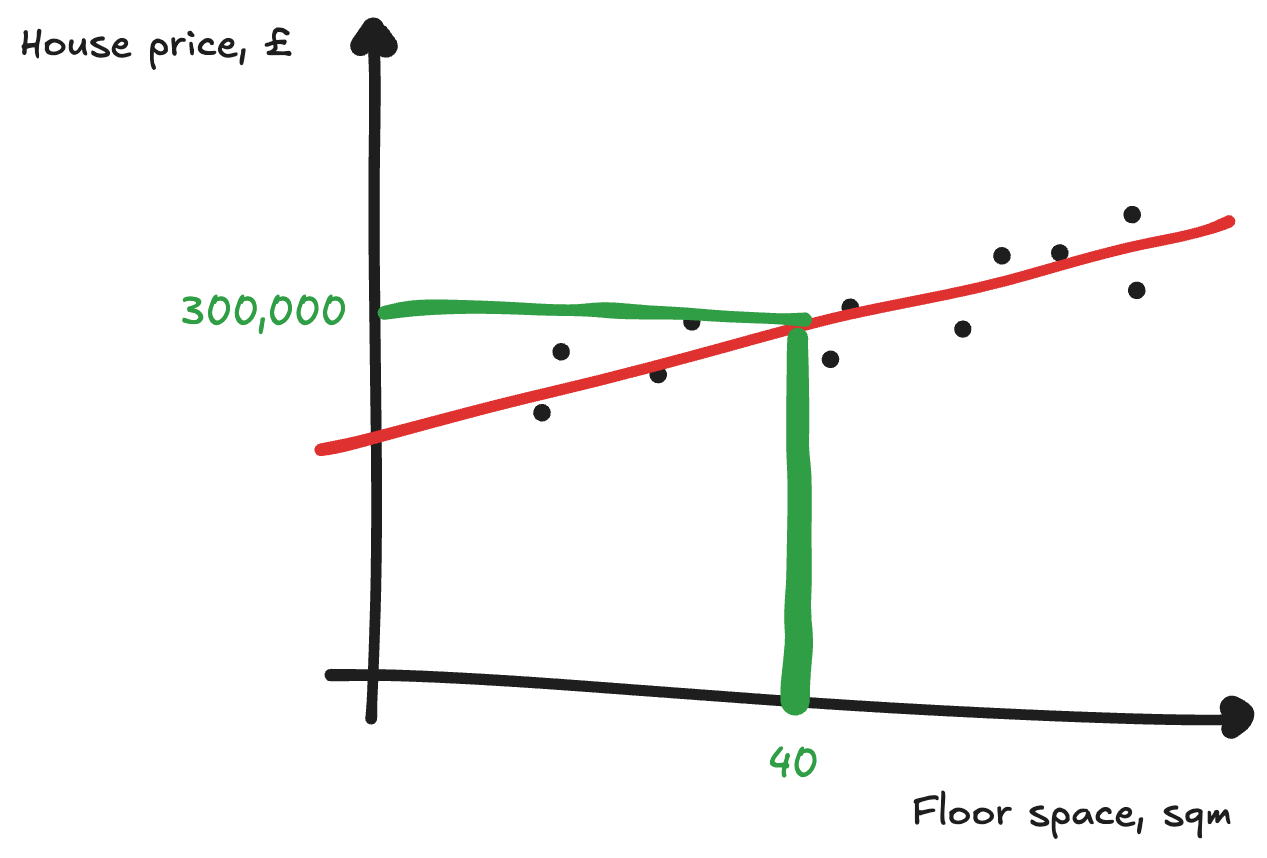
We can repeat this multiple times with both a and b until we get a good line of best fit. Doing this is known as gradient descent, as we’re using the gradient to make our loss function descend. Eventually we end up with an accurate line of best fit:

We can then also see how new houses should be priced. For example, a house of 40 sqm is worth roughly £300,000 with the line of best fit.

What we’ve done here is:

• learned parameters that describe the relationship between the inputs (floor space) and outputs (house price); and

• used the parameters we learned to predict an output given new inputs

While this might seem like a trivial example, this is what most AI systems are doing at their core. And understanding larger AI systems becomes a lot easier if you grasp the above.

Adding more inputs

In the above example, we had just one input. But the same technique scales to many inputs.

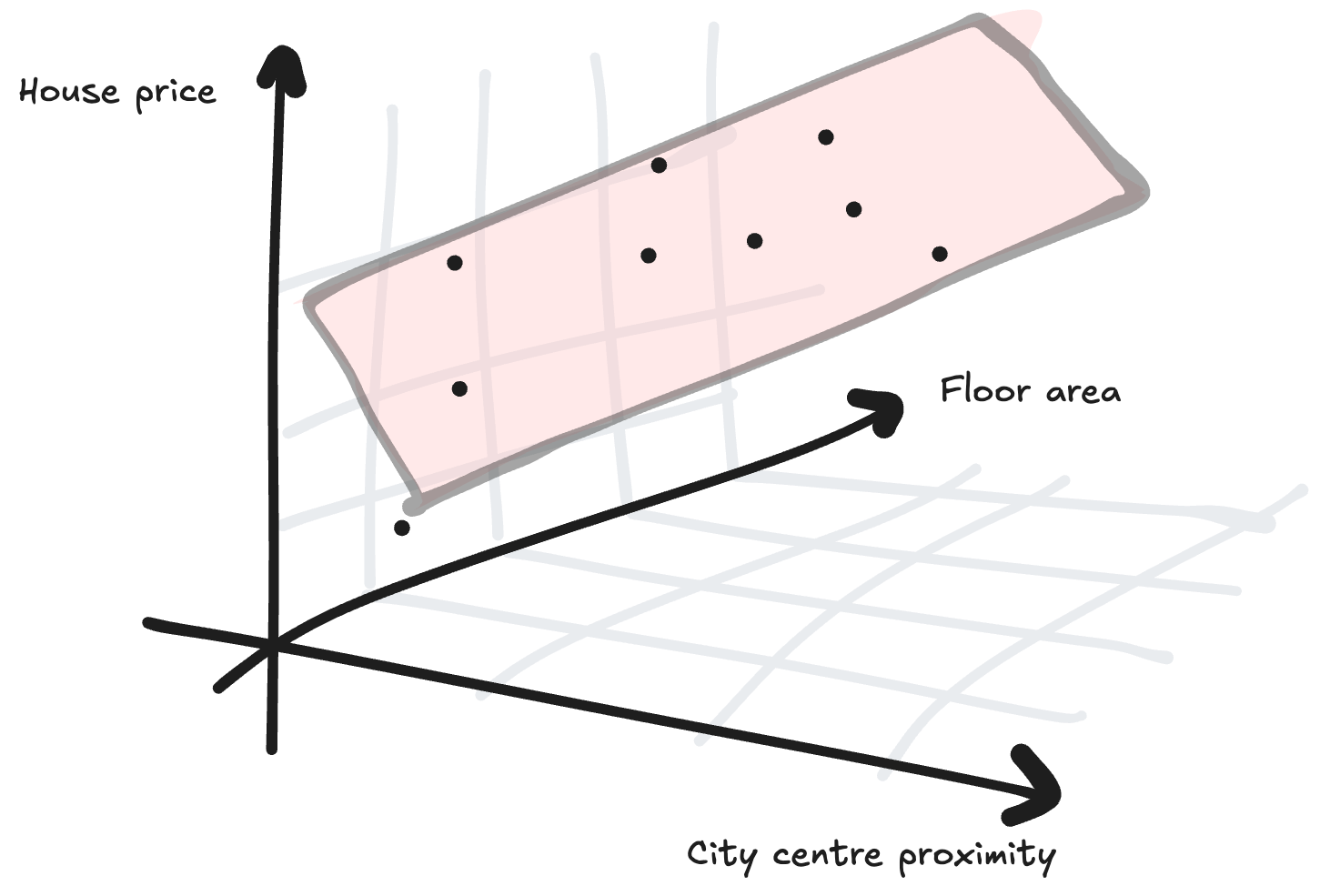
For example, if we had an extra data point about how far the houses were from the city center we could imagine plotting a 3D graph, instead of a 2D one, and drawing a plane of best fit:

The equation for a plane of best fit is z = ax + by + c. We now have three parameters rather than two: a, b and c, because our model is more complex.

We could keep extending this reasoning to handling more and more inputs. While drawing the graphs stops working after a while (e.g. the next level up is a hyperplane in 4D space, rather than 3D space), the underlying maths stays the same.

Fitting more complex data

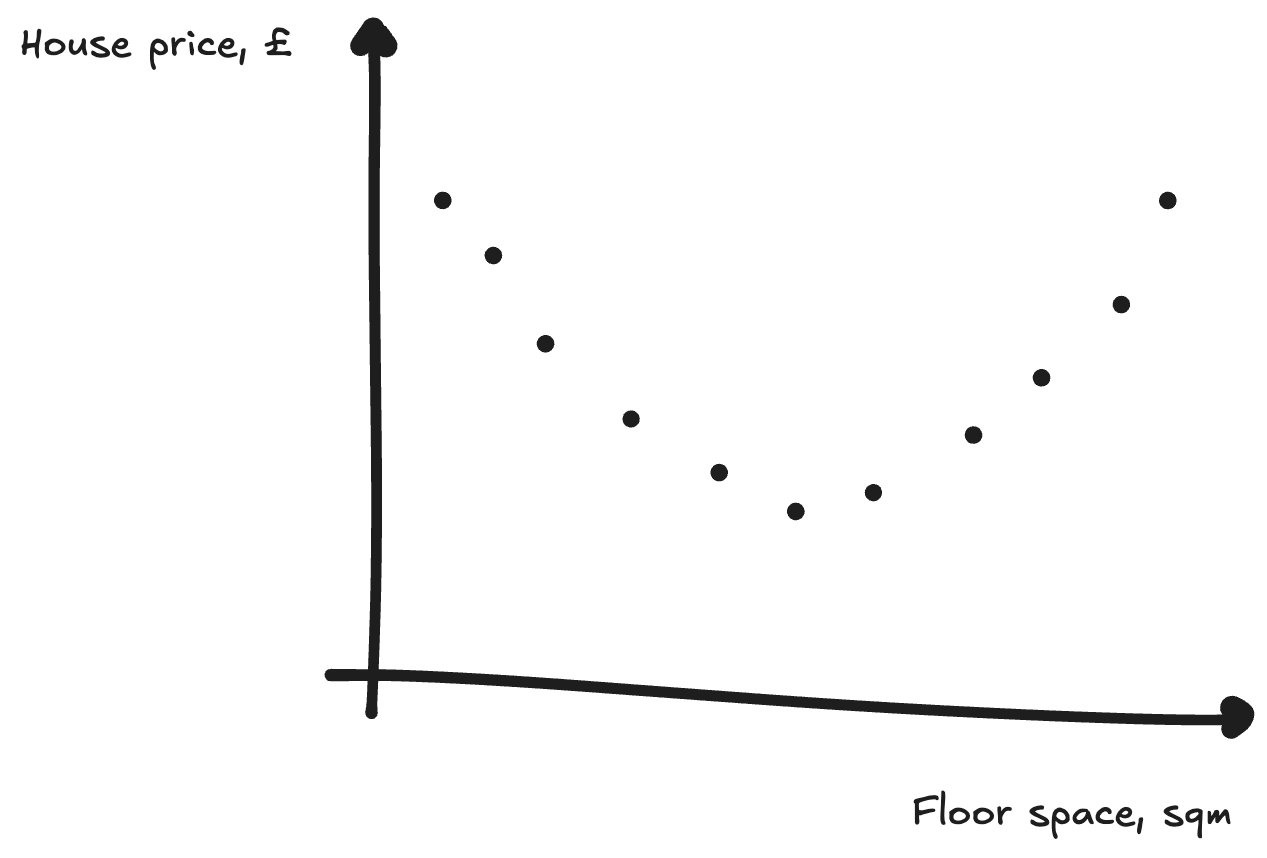
So far, we’ve been fitting a line (or plane, or hyperplane) to our data. This works fine for this simple case, but what if we had data like this:

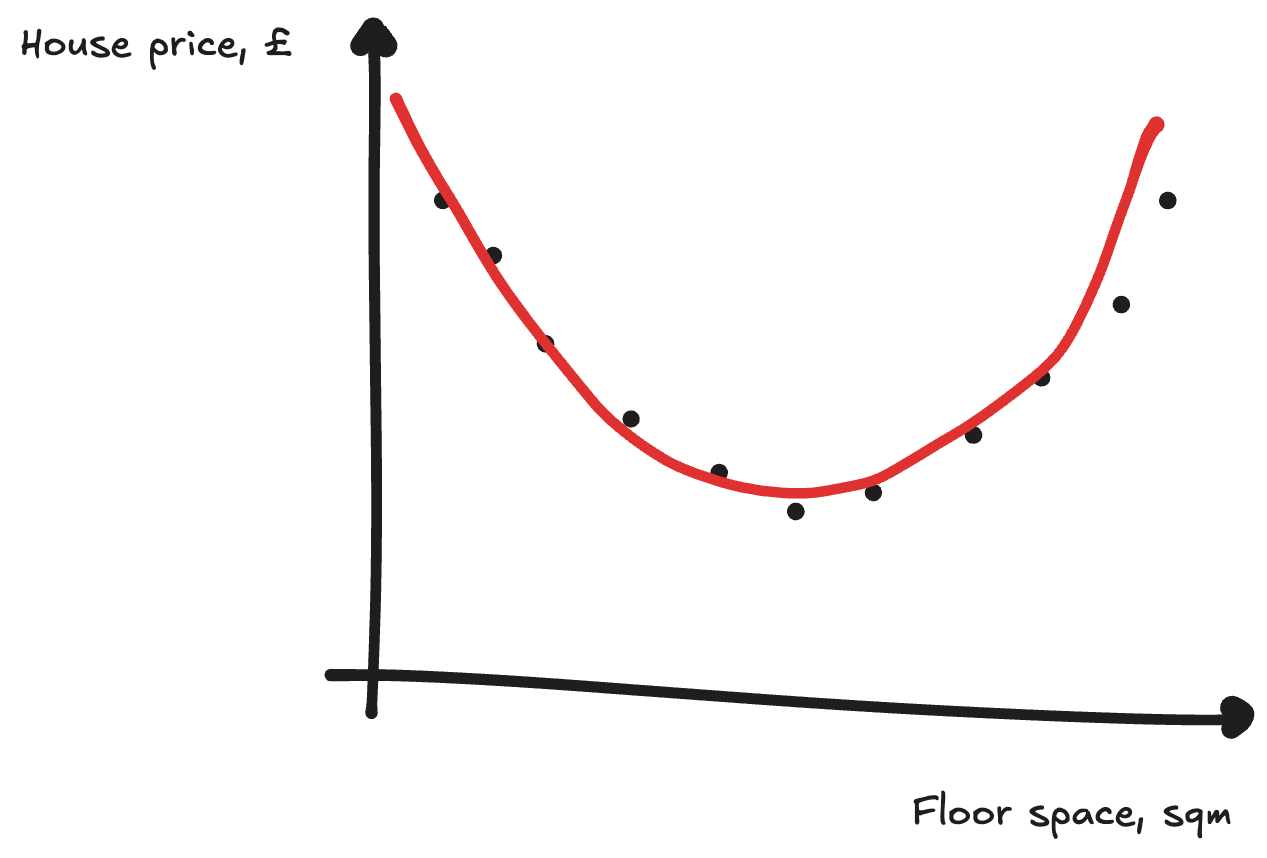
Here, we’d need something more than just a line to predict these points. We might instead use a quadratic equation to fit the data. This also requires more parameters again: y = ax² + bx + c, rather than y = ax + b. But we can use the same gradient descent trick to find the line that fits best - tweaking our parameters to decrease the loss.

The rise of neural networks

Using a quadratic equation got us out of a bind above. But we might have even more chaotic data, or not know what type of equation to use to fit the data beforehand.

To solve this, computer scientists developed a general-purpose tool to fit any data: the neural network. These can approximate any continuous mathematical function, given enough parameters.

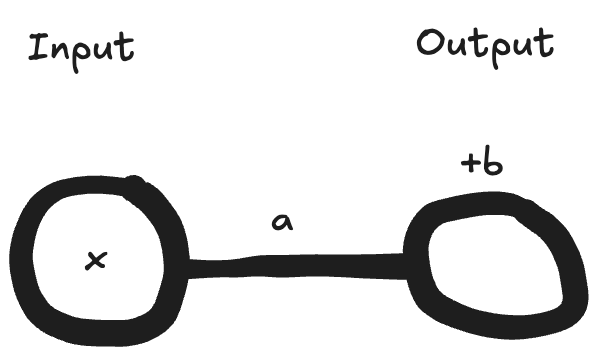
Equations for neural networks can be quite long and complex. We therefore often think about neural networks made of neurons, with values passing through the network from left to right. The most simple network we could have might have just one input neuron and one output neuron:

Each neuron computes a new value (an activation) based on the previous layer’s activations. This involves:

• calculating a weighted sum of the last layer’s activations, and;

• adding a value that biases the neuron to have a lower or higher value.

Each neuron therefore has weights for the weighted sum, and a bias value. These weights and biases are the parameters of the neural network. In the diagram above, x is an activation, a is a weight, and b is bias.

In our simple case above, the equation is actually the same as our line from earlier! The weighted sum of the inputs is our weight (a) times the activation (x), and the bias (b) is a constant, so. Output = ax + b.

This model has just two parameters (one weight and one bias). However, most neural networks are much larger than this - frontier models tend to have billions or even trillions of parameters. This allows them to represent much more complex equations.

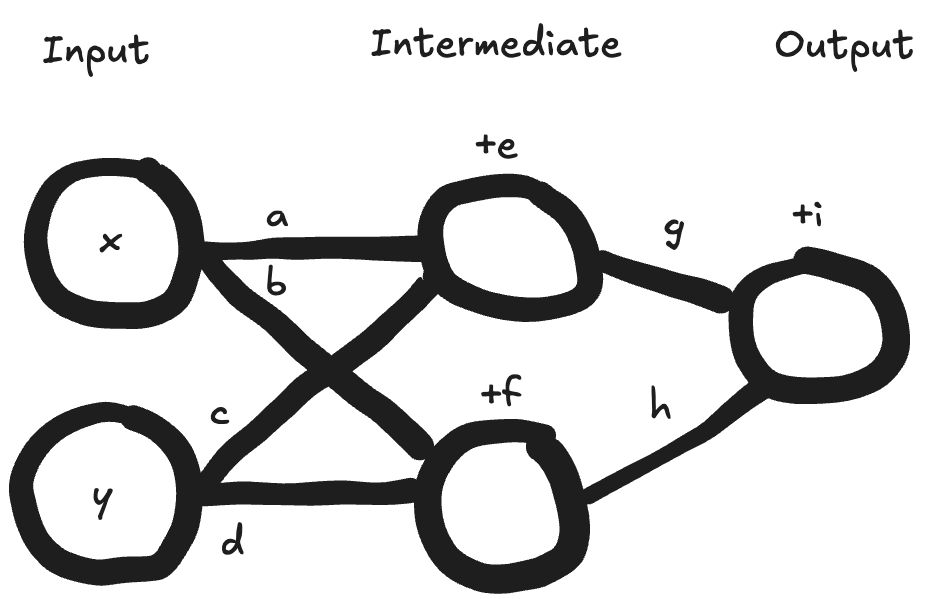
Let’s look at an example with 2 neurons in the input layer, 2 neurons in an intermediate layer, and one output neuron:

What’s the equation for the output here? You can stop to try to work it out yourself if you’d like. (Refer to the key at the bottom of our post, question #1)

Great, so we have the structure.[[3]] But how do we train this?

This is actually very similar to our line fitting from before. We initially start with random parameter values. The structure of a neural network allows us to calculate the gradient,[[4]] the relationship of how changing parameters changes our loss (how far off we were from the correct answer). We can then use gradient descent to repeatedly update the parameters. This reduces the loss, making the neural network predict closer to the correct answers.

This is as far as we’ll explain neural networks here, but if you’d like to learn more (or just have this explained in another way) we recommend 3Blue1Brown’s YouTube series on neural networks.

Using our general function fitters

Tuning parameters with gradient descent to fit data forms the foundation for almost all modern AI systems. Let’s see how this approach works for a number of different AI use cases. To learn best, try guessing how you might solve each problem before opening the answer.

House price prediction is a fairly narrow task (as opposed to something more general, like ChatGPT being able to answer questions on anything). Here, our inputs were the properties of the house and the target output was the house price, for example:

BedroomsBathroomsFloor space (m²)To city center (km)House Price (£)11451.3375,00021654.5550,000

Given the above example for house price prediction for estate agents, can you guess how you might build an AI to detect fraudulent card payments at a bank? (Question 2)

AI can also process other types of data. Image classification models enable apps like Google Photos use to categorise your photos by subject. How might we build these? (Question 3)

Making things more general, we can look at large language models. This includes models such as ChatGPT, which can answer queries and output text responses. The first step of creating these models involves being able to autocomplete internet text. What might the dataset look like for these? (Question 4)

What about for other output modalities? Try coming up with a way we might train image generation models. (Question 5)

Finally, reinforcement learning is a powerful technique where we specify successful outcomes for the AI system (such as getting a high score in a video game), but don’t specify exactly what the AI system should do to achieve that goal (the buttons to press etc.).

This is useful because for it allows the AI system some creativity in how to achieve the goal, which often discovers new solutions.

AlphaGo was trained using reinforcement learning to play the board game Go. This AI system beat Go world champions - not by trying to autocomplete human moves, but by playing against itself and with the successful outcome being specified as winning a game. This enabled it to make moves like the famous “move 37”, which confused humans initially but people later realised was a strong move.

How might the dataset look for this? (Question 6)

Why now? Compute, data and algorithms

Many of the above ideas were around in 1943, and people ran them on computers in 1967. So why didn’t we have ChatGPT decades ago?

This is because developing AI depends on three key factors: compute, data, and algorithms. We had the algorithms piece with neural networks, but only recently started applying much more compute to learn from much more data.

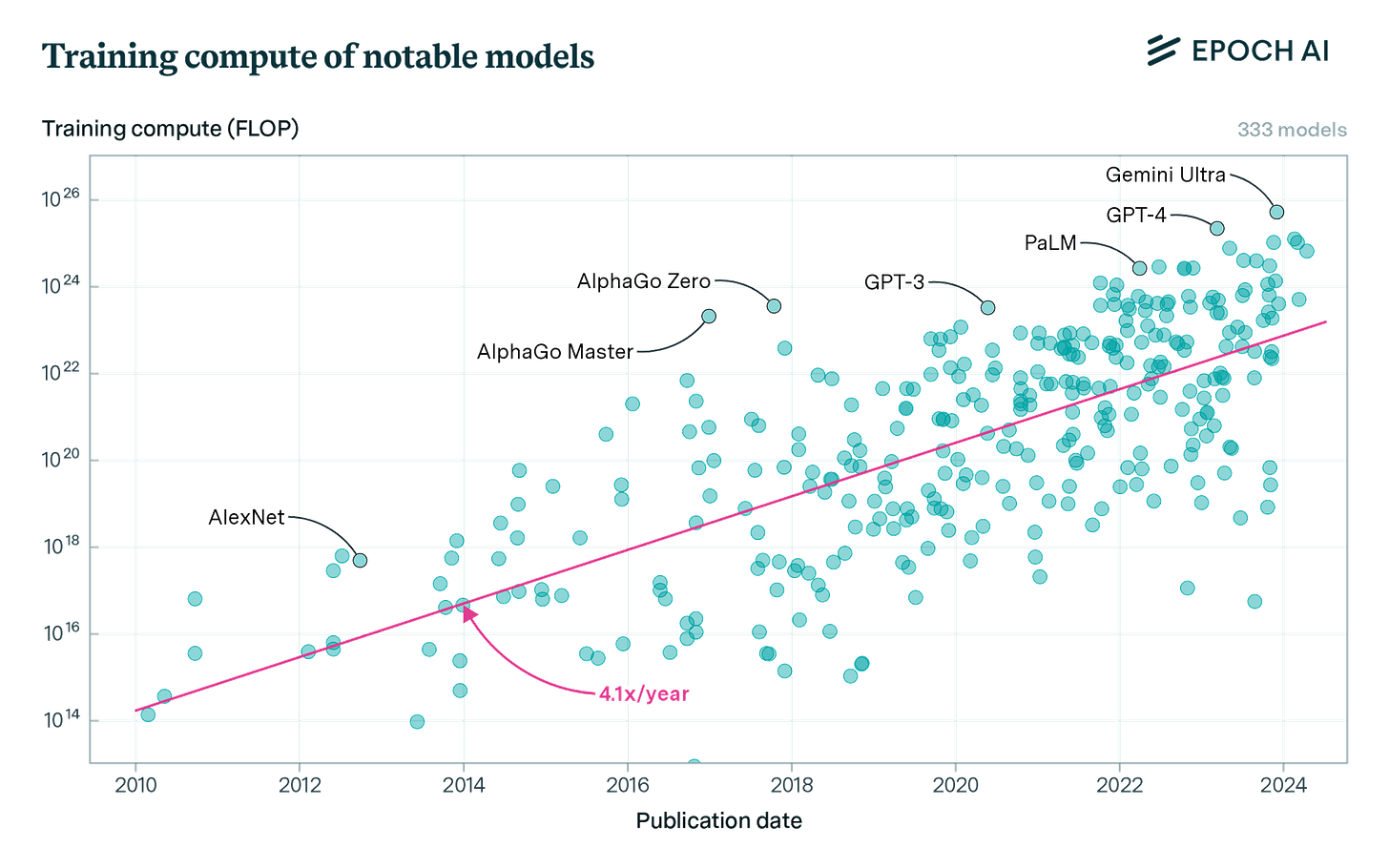
Chart: Training compute of notable models has increased by ~1,500,000,000x from 2010 to 2024. Source: Epoch AI, licensed under CC-BY.

Compute refers to the raw computational power needed to train AI systems. Remember how we had to try many small parameter adjustments to fit our line to the house price data? Modern AI systems do this billions of times with trillions of parameters. To recalculate the gradient and loss for so many parameters requires enormous computing power doing lots of little calculations, typically provided by specialized AI chips in large data centers.

Data is equally important. Just as our house price predictions would improve with more examples (particularly if it was a complex equation, rather than just a line), AI systems generally get better at fitting patterns when trained on more data. But quantity isn’t everything - quality matters too. An LLM trained to autocomplete text from random people on Twitter will provide much less accurate (although probably more humorous) health advice than one trained on text from medical textbooks.

Algorithmic improvements also advance AI. This can directly affect capabilities, such as how moving from linear equations to neural networks allowed us to capture more complex patterns. Better algorithms can also boost AI by letting us use compute and data more efficiently: for example, the transformer architecture (introduced in 2017) allowed AI systems to process information more efficiently in parallel, making much better use of available computing power. This in turn enabled us to process much more data, up to huge amounts of the internet, unlocking the training of large language models.

Recap

• AI models learn from data by adjusting parameters with gradient descent.

• Most AI development uses neural networks because they can represent a wide range of different equations.

• These techniques can solve many tasks, from narrow classifiers to fairly general text and image generation systems.

• However, these rely on having sufficient compute and data to train systems. Better algorithms can help us make training more effective given the compute and data we do have.

---

Answer [1]: Output = g × (ax + cy + e) + h × (bx + dy + f) + i

Answer [2]: One way you might do this is training a neural network on the data from previous card transactions, and whether they were recorded as fraud afterwards. This training process will update the parameters of the neural network (the weights and biases) with gradient descent, so that it gets good at predicting whether a transaction was fraudulent or not. We might need to convert some of the data into numbers, such as a yes/no fraud flag into a percentage, or the day of week into a number between 1 and 7.

| Transaction amount | Account balance | Day of week | Fraud likelihood |

|------------------------|---------------------|-----------------|----------------------|

| 124.37 | 2033.78 | 2 | 0% |

| 99.99 | 1093.20 | 4 | 100% |

When a new transaction comes in, we can run it through the model and predict its fraud likelihood. If it’s then above a certain limit, we might block it or flag it for human review.

Answer [3]: We can use a similar trick as we did for the fraud likelihood in the last example to convert data into numbers. Any data you can have on a computer is represented as 0s and 1s in the end, so must be possible to convert to a number somehow. For images, each pixel in an image already has numerical values representing its color (typically from 0 to 255 for each of red, green, and blue). So we can standardise the input size, we might resize the image to fixed dimensions before putting it in the model, say 1000x1000 (so there are 1 million pixels total). We can also output the category as a number, where perhaps 1 = dog, 2 = cat, 3 = … etc. The neural network can then learn the patterns that distinguish, say, pictures of cats from pictures of dogs.

| Pixel 1 red color | Pixel 1 green color | Pixel 1 blue color | (other pixels) | Pixel 1,000,000 blue color | Image category |

|-------------------|---------------------|--------------------|----------------|----------------------------|----------------|

| 234 | 82 | 80 | … | 162 | 2 |

| 26 | 195 | 152 | … | 139 | 1 |

Alternatively, as neural networks can have multiple output neurons, we can have an output for each option. We might pick this because it just happens to have better performance, or because it allows us to handle images with multiple objects (e.g. an image of a cat and dog together). The data for this would look like:

| Pixel 1 red color | (other pixels) | Likelihood contains dog | Likelihood contains cat | (other outputs) |

|-------------------|----------------|-------------------------|-------------------------|-----------------|

| 234 | … | 0% | 100% | … |

| 26 | … | 100% | 0% | … |

Answer [4]: First, we need to find lots of data as examples. Most AI companies download large parts of the internet and copy the text to learn from. We can then take snippets of this text, and get the neural network to predict the next word. For example:

| Word 1 | Word 2 | Word 3 | Word 4 | Next word |

|--------|--------|------------|----------|-----------|

| First | we | need | to | find |

| Most | AI | companies | download | large |

To convert things into numbers, we use a similar trick to our image classification model: set up a mapping from category to number. For example, AI = 1, companies = 2, download = 3. We might have:

| Word 1 | Word 2 | Word 3 | Word 4 | Next word |

|--------|--------|--------|--------|-----------|

| 5 | 10 | 8 | 9 | 4 |

| 7 | 1 | 2 | 3 | 6 |

Now when we have new text to complete, such as “Human: Tell me a joke, Assistant: “, these can be converted into numbers and the AI can predict a reasonable next word. Repeatedly doing this results in an entire response being produced by the AI.

Early versions of AI systems trained this way were used to provide autocomplete suggestions on phones. But it turns out that when trained on vast amounts of text from the internet, these models learn not just vocabulary and grammar, but also patterns about how ideas relate to each other.

While predicting the next word might seem simple, this can enable AI systems to engage in complex dialogue and appear to reason.

(In reality, we often break things down into a finite set of tokens rather than just words, use vectors rather than single numbers, and use other techniques such as attention that make learning more effective or parallelisable. But the core principle is the same.)

Answer [5]: We can use the dataset for our image classification model, but in reverse.

We can also use the techniques we learnt from making large language models to convert words or concepts into numbers, and pass them in to the model as input.

| Word 1 | Word 2 | Word 3 | Image pixels (many outputs) |

|---------------|--------------|---------------|-----------------------------|

| 3 (dog) | 17 (grass) | 78 (ball) | … |

| 99 (windmill) | 17 (grass) | 51 (bicycle) | … |

(In practice, there are more efficient ways to structure datasets to train AI models to do this, usually involving adding and removing noise. If you’d like to learn more, you can refer to this video.

Answer [6]: Here, the training data looks a little different from our previous examples. Rather than predicting the next action, we predict the how good taking an action will be. We’ll call this the ‘reward’.

| Game state | Action taken | Reward |

|---------------|----------------------|--------------------------|

| Empty board | Place stone at D4 | +1.0 (eventual win) |

| Stone at D4 | Place stone at Q16 | -1.0 (eventual loss) |

As the AI is playing the game, we actually don’t know what the eventual outcome or reward is. So we store the first two columns in the dataset, but the reward column is blank. Only at the end of the game, can we work backwards and assign an outcome and corresponding reward to the actions.

Now we can train a model to predict a reward for an action, or a ‘reward model’.

Once we have this reward model, we can use it to play better in future. To do this, we list all the possible moves, use the reward model to estimate how good they are, and pick the one with the highest expected reward. Doing this will make it more likely that we win the game.

We can do this entire loop several times, with the AI learning after each game. As we do this, the AI learns better strategies to make more winning moves. We also don’t need to play against the AI ourselves - we could set up two copies of the AI play against each other millions of times to generate lots of example data, known as self-play.